University of Massachusetts
Manning College of Information and Computer Sciences

University of Massachusetts
Manning College of Information and Computer Sciences
With 2021 drawing to a close, we would like to take a moment to recognize the wealth of machine learning research produced by the UMass Manning College of Information and Computer Sciences (CICS). This retrospective provides a brief summary of many (not all) of the machine learning papers published by students and/or faculty in CICS. You can browse papers by their name in the index below, or can just scroll through to get a sense for all of the work that we are doing!
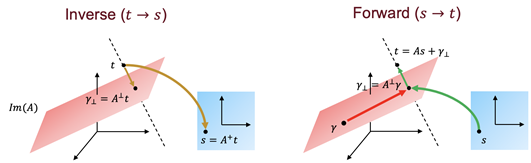
[AISTATS 2021] RealMVP: A Change of Variables Method For Rectangular Matrix-Vector Products.
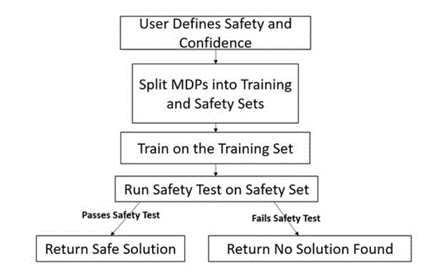
[ICML 2021] High Confidence Generalization for Reinforcement Learning.
[ICML 2021] On the Difficulty of Unbiased Alpha Divergence Minimization.
[ICML 2021] Posterior Value Functions: Hindsight Baselines for Policy Gradient Methods.
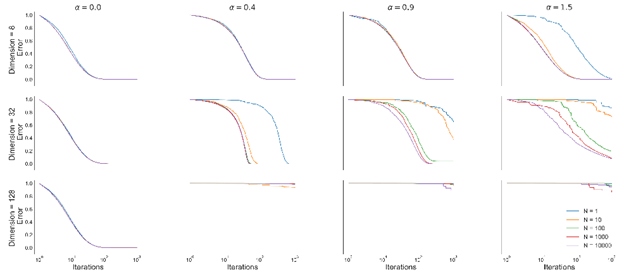
[ICML 2021] Towards Practical Mean Bounds for Small Samples.
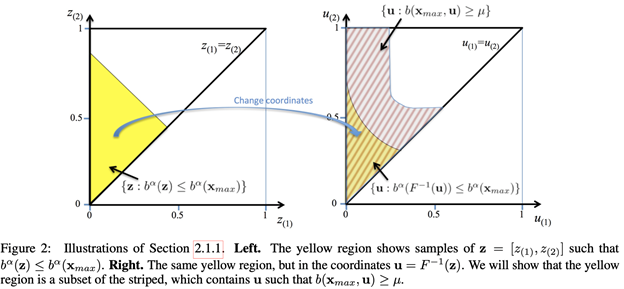
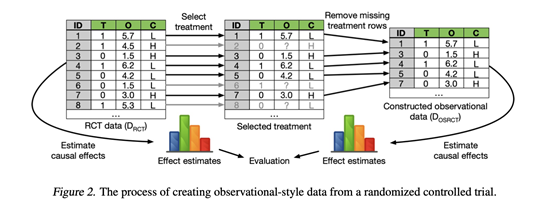
[ICML 2021] How and Why to Use Experimental Data to Evaluate Methods for Observational Causal Inference.
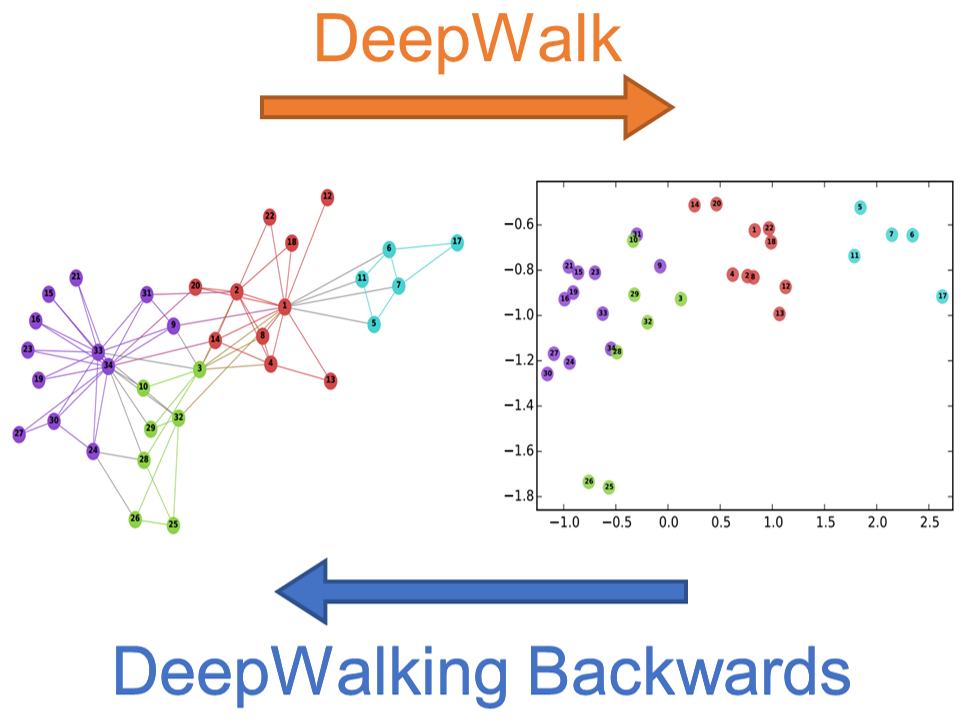
[ICML 2021] DeepWalking Backwards: From Node Embeddings Back to Graphs.
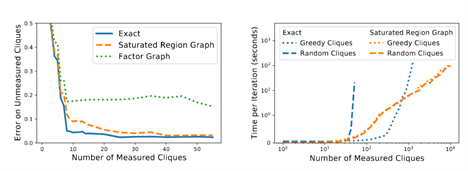
[ICML 2021] Faster Kernel Matrix Algebra via Density Estimation.
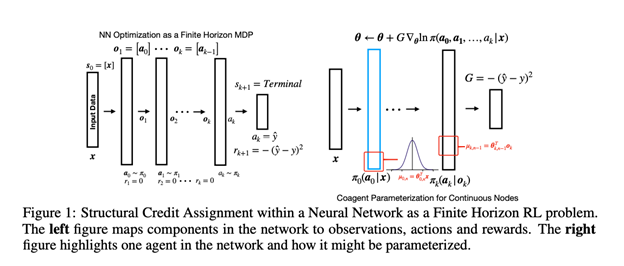
[NeurIPS 2021] Structural Credit Assignment in Neural Networks using Reinforcement Learning.
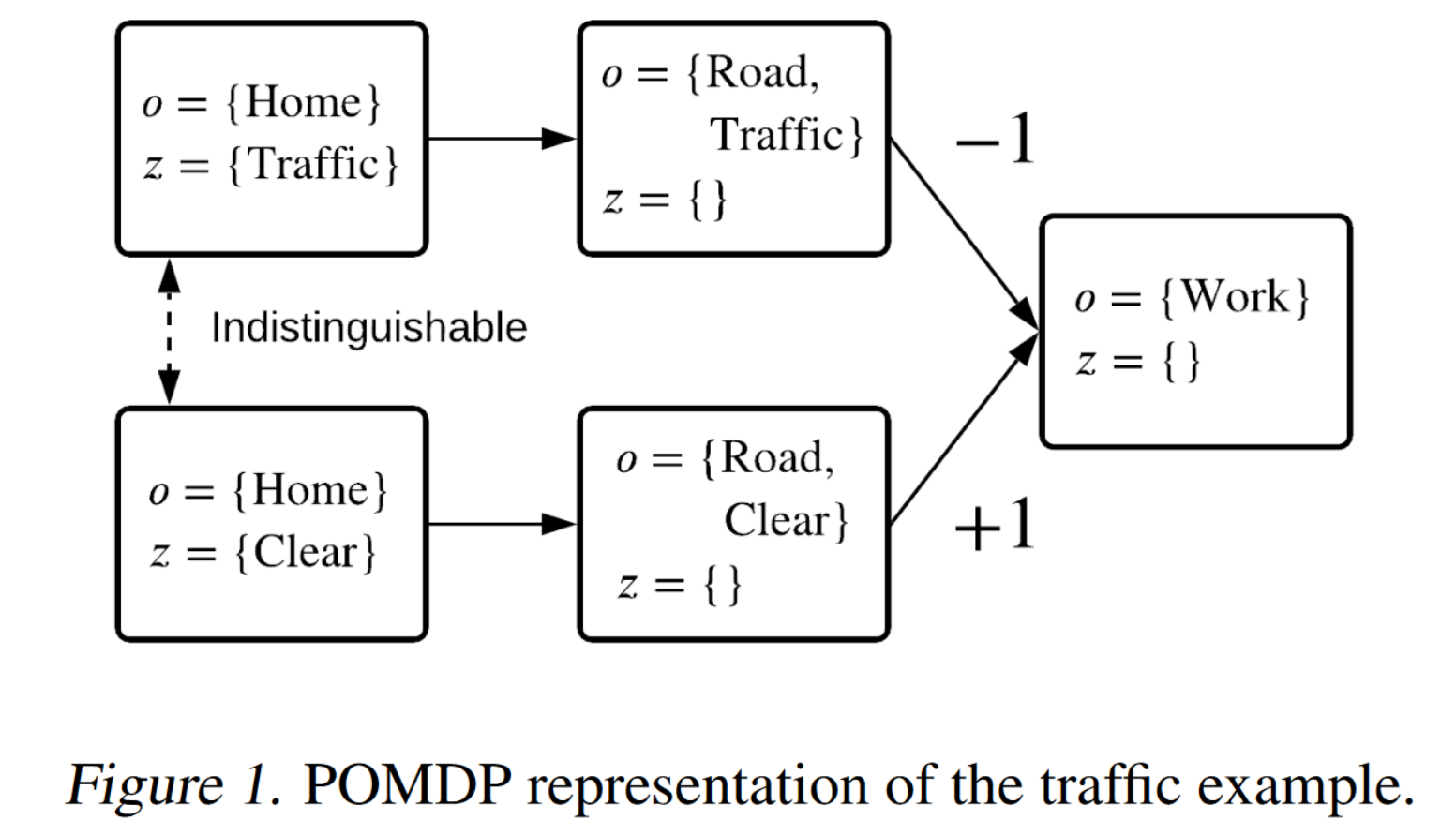
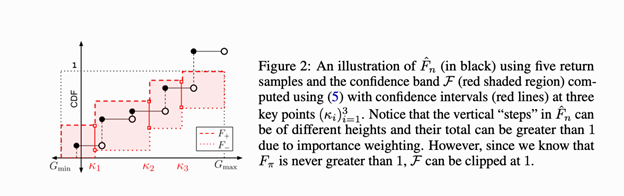
[NeurIPS 2021] Universal Off-Policy Evaluation.
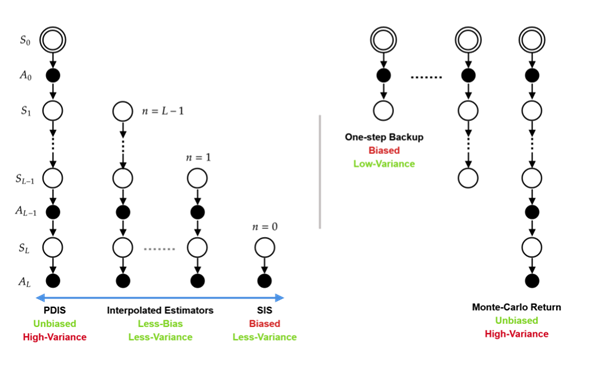
[NeurIPS 2021] SOPE: Spectrum of Off-Policy Estimators.
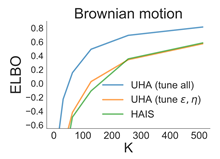
[NeurIPS 2021] MCMC Variational Inference via Uncorrected Hamiltonian Annealing.
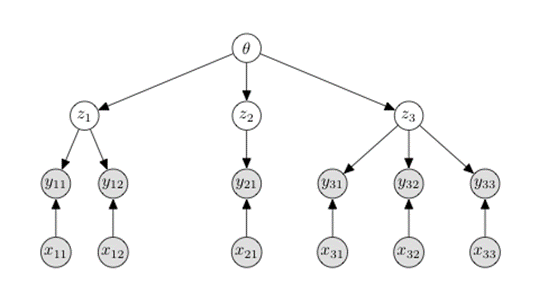
[NeurIPS 2021] Amortized Variational Inference for Simple Hierarchical Models.
[NeurIPS 2021] Relaxed Marginal Consistency for Differentially Private Query Answering.
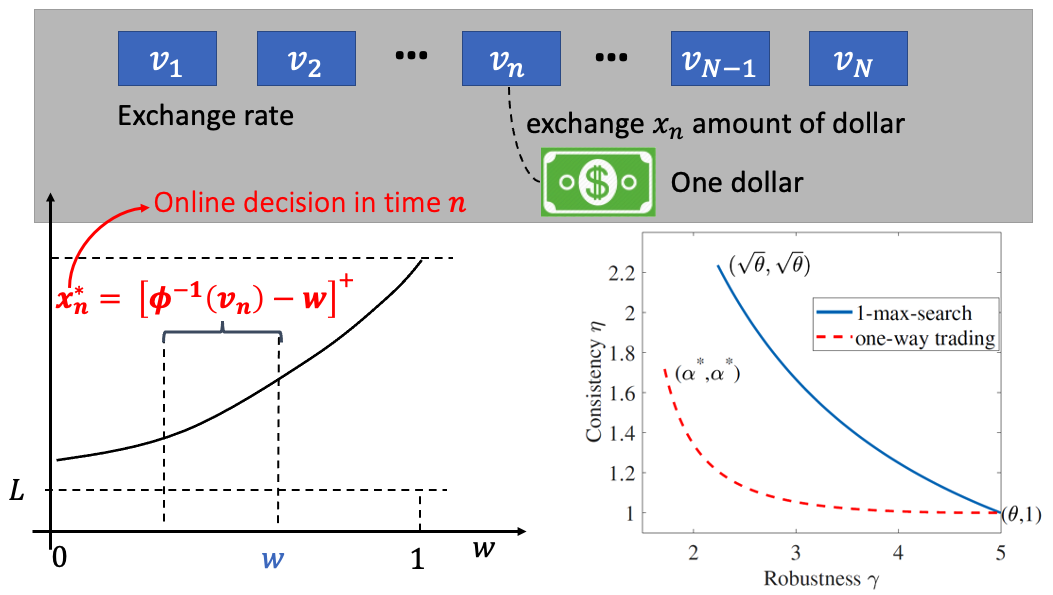
[NeurIPS 2021] Pareto-Optimal Learning-Augmented Algorithms for Online Conversion Problems.
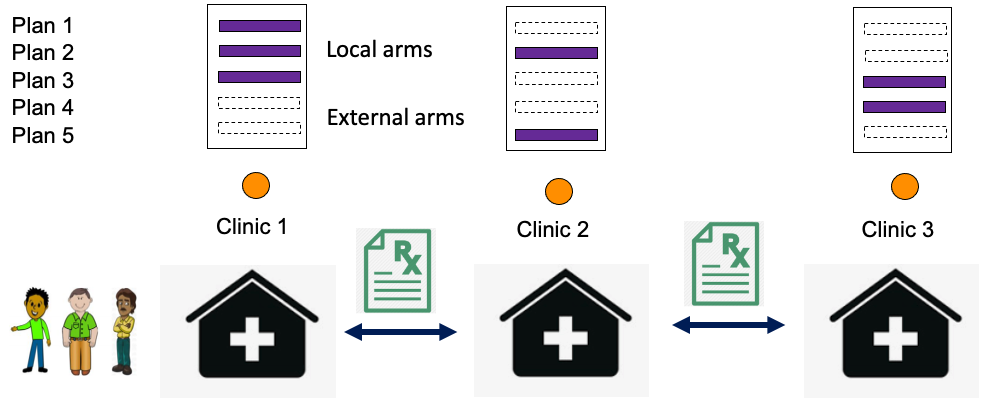
[NeurIPS 2021] Cooperative Stochastic Bandits with Asynchronous Agents and Constrained Feedback.
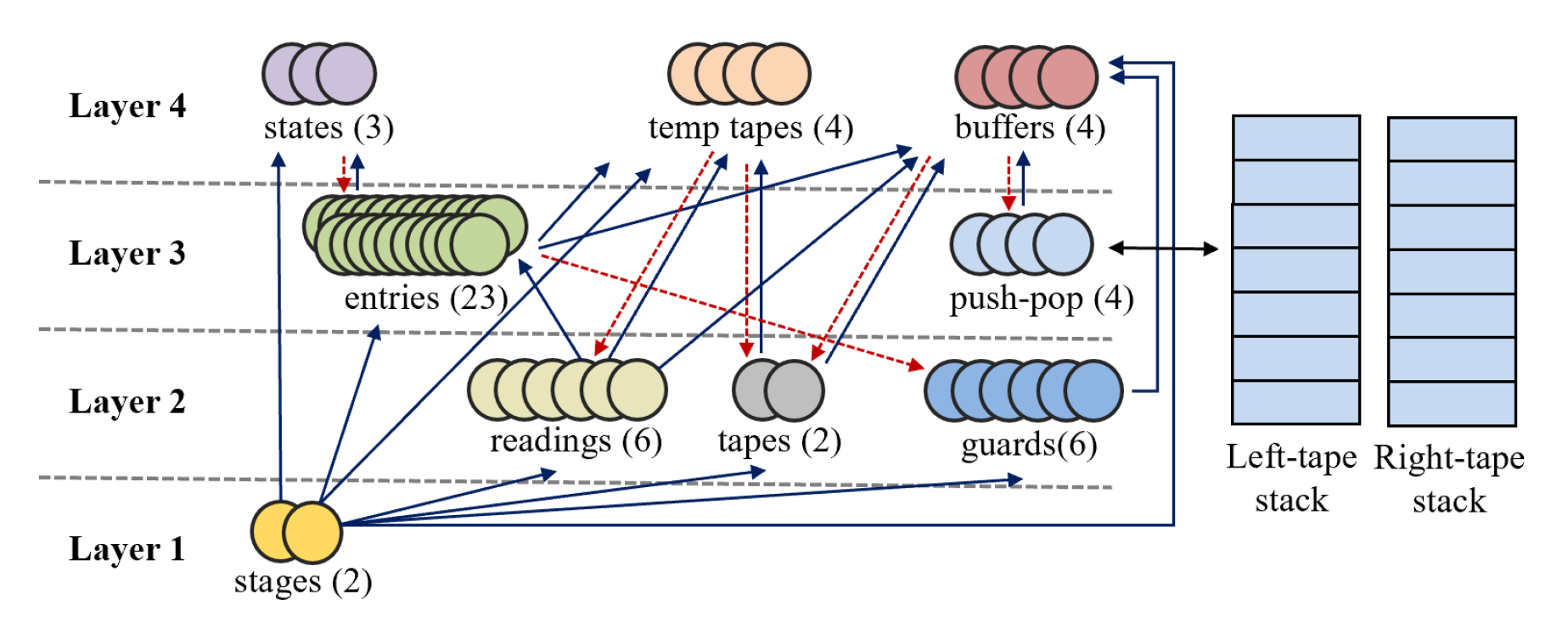
[NeurIPS 2021] Turing Completeness of Bounded-Precision Recurrent Neural Networks.
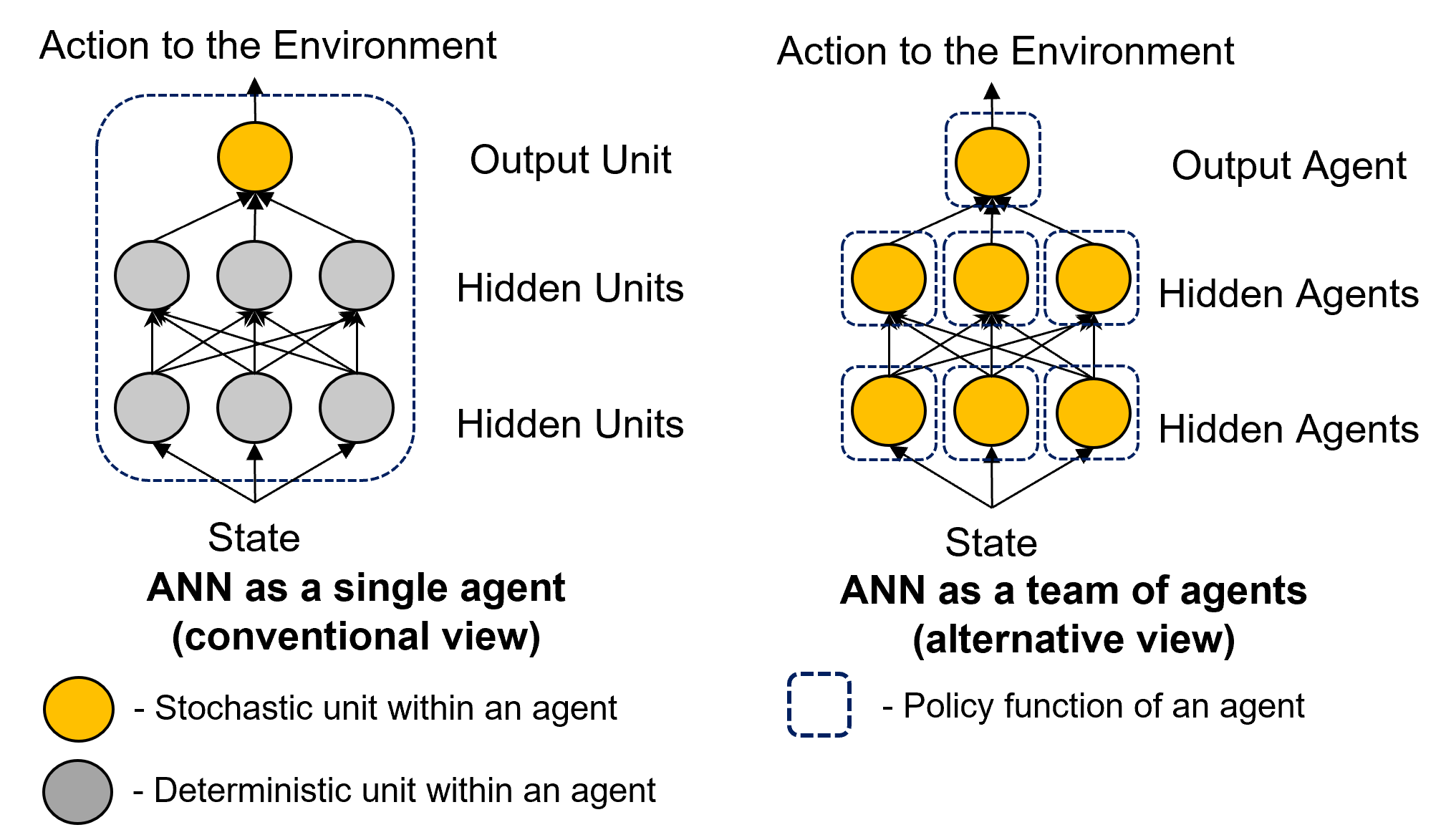
[NeurIPS 2021] MAP Propagation Algorithm: Faster Learning with a Team of Reinforcement Learning Agents.
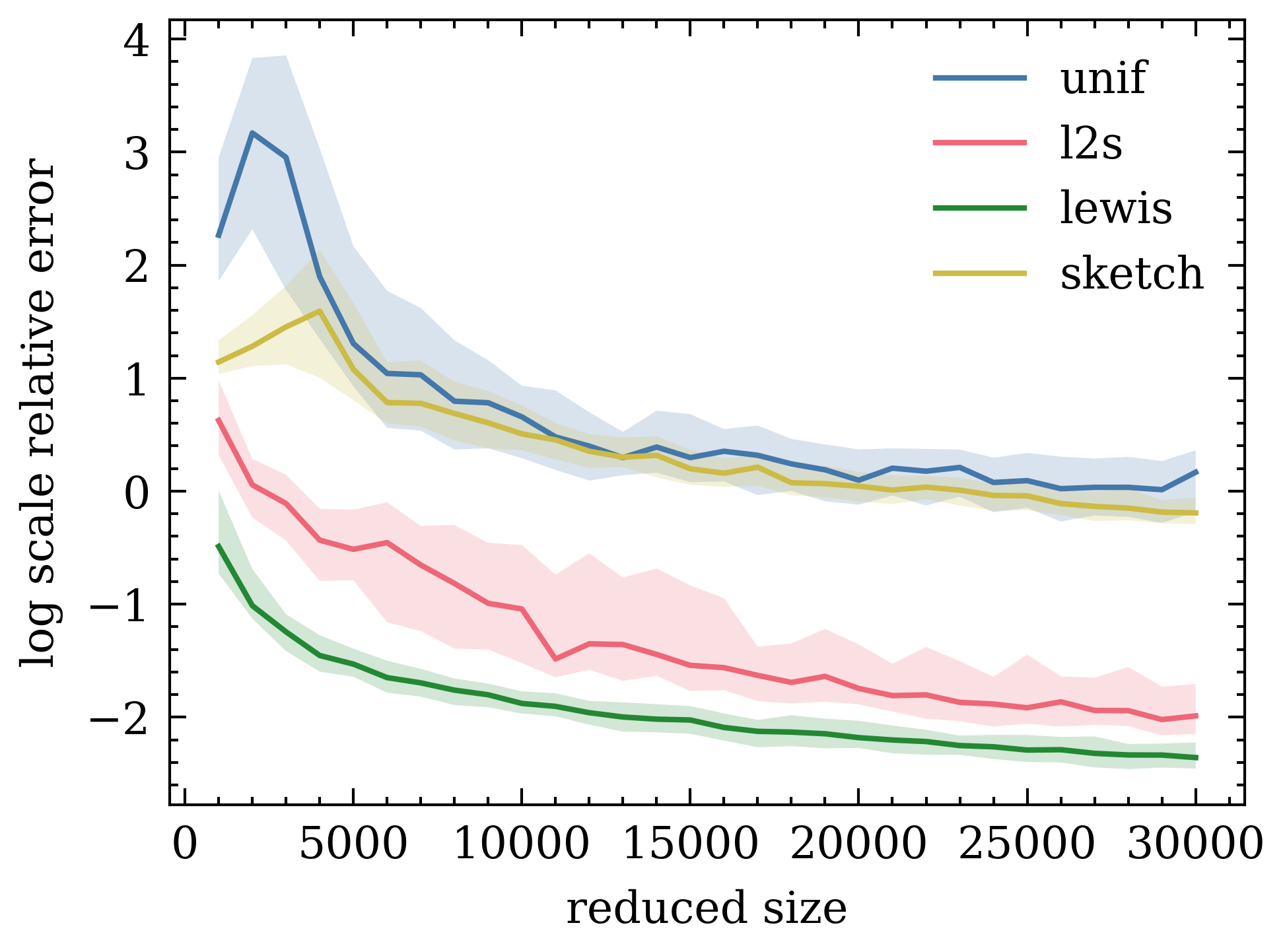
[NeurIPS 2021] Coresets for Classification – Simplified and Strengthened.